Đo góc tiếp xúc và độ nhám – Phải làm gì nếu không có phương trình Wenzel?

Thực tế là độ nhám của bề mặt có thể ảnh hưởng đến tính thấm ướt của nó đã được Wenzel biết rõ và mô tả bằng một phương trình đơn giản. Nhưng lý thuyết này có thể được áp dụng vào thực tế công nghiệp tốt đến mức nào? Kruss đã thực hiện thử nghiệm và tạo ra các tấm silicon có cấu trúc vi mô rất chính xác bằng cách khắc ion phản ứng, nhưng không làm thay đổi cấu trúc hóa học của bề mặt và do đó không làm thay đổi năng lượng tự do trên bề mặt của nó .

Cấu trúc vi mô của các bề mặt được đo bằng kính hiển vi đồng tiêu để xác định các thông số liên quan đến lý thuyết của Wenzel. Các phép đo góc tiếp xúc trên các mẫu có cấu trúc khác nhau cho thấy mối tương quan trái ngược với dự đoán của Wenzel một cách đáng ngạc nhiên. Ví dụ này cho thấy rằng việc hiệu chỉnh dữ liệu góc tiếp xúc, sử dụng các giả định của Wenzel làm cơ sở duy nhất, là không nên. Tuy nhiên, bằng cách đo cả độ nhám và góc tiếp xúc, một giải pháp thực nghiệm thường có thể được tìm thấy trong thực tế để điều tra riêng biệt và cuối cùng dự đoán tác động của độ nhám và năng lượng tự do bề mặt lên khả năng thấm ướt

Giới thiệu

Làm ướt các bề mặt có cấu trúc – trạng thái Cassie-Baxter và Wenzel

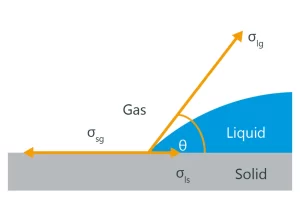
Ngoài thành phần hóa học, địa hình cũng có ảnh hưởng đến đặc tính làm ướt của bề mặt. Có sự khác biệt giữa hai trường hợp: Nếu chất lỏng của giọt được áp dụng thấm vào các cấu trúc (vi mô) và chiếm chỗ không khí trong chúng, thì đây được gọi là trạng thái Wenzel (Hình 1, bên trái). Nếu các thể vùi không khí vẫn còn trong cấu trúc thì trạng thái này được gọi là trạng thái Cassie-Baxter (Hình 1, bên phải).

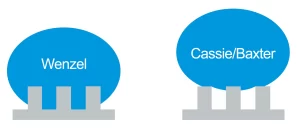
Trạng thái nào hiện diện phụ thuộc vào kích thước và hình dạng của cấu trúc, năng lượng tự do bề mặt của vật liệu cơ bản và sức căng bề mặt của chất lỏng.

Theo Wenzel, mối quan hệ sau đây áp dụng giữa góc tiếp xúc của Young θ trên bề mặt không có cấu trúc và góc tiếp xúc θ* trên bề mặt có cấu trúc của cùng một vật liệu:

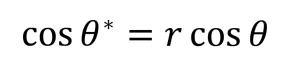
trong đó hệ số nhám r mô tả độ nhám bề mặt và tương ứng với tỷ lệ giữa bề mặt hình học và bề mặt chiếu của các cấu trúc vi mô:

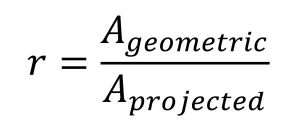
Vì bề mặt được chiếu không thể lớn hơn bề mặt hình học nên r luôn ≥ 1. Theo phương trình Wenzel, góc tiếp xúc trở nên nhỏ hơn dưới 90° và lớn hơn trên 90° do cấu trúc. 90° đồng thời là góc giới hạn của khả năng thấm ướt , do đó các vật liệu hút ẩm thậm chí còn trở nên hút ẩm hơn và các vật liệu kỵ nước thậm chí còn kỵ ẩm hơn.

Xem xét các phương trình này, rõ ràng có thể dễ dàng dự đoán khả năng thấm ướt của các bề mặt có cấu trúc nếu biết θ và r . Ngược lại, có thể xác định tác động tương ứng của các quy trình kỹ thuật như phun cát hoặc kích hoạt plasma lên độ nhám bề mặt (r) và hóa học bề mặt dưới dạng góc tiếp xúc trên bề mặt nhẵn (θ). Liệu phương trình Wenzel có cho phép hiệu chỉnh trực tiếp như vậy trong thực tế hay không đã được chúng tôi nghiên cứu trong bối cảnh của báo cáo này.

Thí nghiệm đo góc tiếp xúc và độ nhám

Chuẩn bị mẫu

Ở dạng rắn, công ty 5microns GmbH (Ilmenau, Đức) đã cưa các con chip có cấu trúc khác nhau từ một tấm bán dẫn silicon. Các cấu trúc được hiện thực hóa một cách dị hướng bằng phương pháp ăn mòn ion phản ứng. Sơ đồ biểu diễn các chip silicon có cấu trúc được hiển thị trong Hình 2. Các cấu trúc mở, trái ngược với các cấu trúc đóng, có cấu trúc nghịch đảo cho phép không khí thoát ra khi bị chất lỏng làm ướt. Chiều rộng rãnh A thay đổi từ 5 đến 50 µm, kích thước cấu trúc B từ 10 đến 50 µm. Độ sâu mục tiêu của các cấu trúc là 5 µm mỗi cấu trúc. Bất kể cấu trúc mục tiêu là gì, tất cả các mẫu đều có cấu trúc bề mặt đồng nhất, giống nhau (silicon dioxide).

Hệ số nhám r đối với kết cấu sử dụng được tính theo:

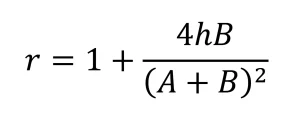
Phân tích cấu trúc bề mặt

Cấu trúc bề mặt của chip silicon được đo bằng kính hiển vi đồng tiêu Twip Consigno. Với thiết bị này, việc sử dụng kỹ thuật vi thấu kính cho phép hiệu suất ánh sáng cao, có nghĩa là có thể đo được các mẫu rất tối hoặc thậm chí trong suốt với độ phân giải trục cao. Các phương pháp phổ biến khác, chẳng hạn như phép đạc tam giác/chiếu ánh sáng sọc, bị hạn chế trong ứng dụng của chúng, ví dụ bằng cách giảm phạm vi đo chiều cao trong khi vẫn duy trì độ phân giải thấp, do các vấn đề với các mẫu phản chiếu khác nhau và do hiệu ứng “bóng mờ”, nhờ đó các cấu trúc có thể bị ẩn đi và do đó bị bỏ qua. Các phép đo được thực hiện với vật kính có độ phóng đại 100 lần. Mỗi vùng được quét có kích thước 0,19 × 0,15 mm2 với phạm vi chiều cao là 15 µm. Đối với các phép đo, phần mềm “itom” đã được sử dụng. Để xác định r , bộ lọc cắt độ nhám 0,8 µm được áp dụng cho hình ảnh thu được.

Đo góc tiếp xúc

Các phép đo góc tiếp xúc được thực hiện bằng Máy đo góc tiếp xúc KRÜSS DSA100, sử dụng phần mềm ADVANCE. Với mục đích này, năm giọt nước cất kép được đặt trên mỗi con chip với sự hỗ trợ của hệ thống định lượng kim được điều khiển bằng phần mềm và góc tiếp xúc cân bằng (CA) của chúng đã được xác định. Thể tích nhỏ giọt là 2 µL, tất cả các phép đo được thực hiện ở 23 ± 0,5 °C. Kết quả là giá trị trung bình với độ lệch chuẩn cho tất cả các giá trị hydrocarbon trên mỗi mẫu.

Kết quả

Hệ số độ nhám r được tính toán và đo

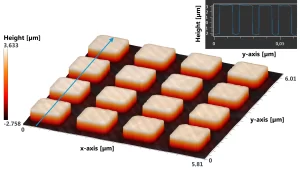
Hình 3 thể hiện địa hình bề mặt của một mẫu có cấu trúc vi mô mẫu. Kích thước của cấu trúc tương ứng tốt với kích thước do nhà sản xuất 5microns GmbH chỉ định.

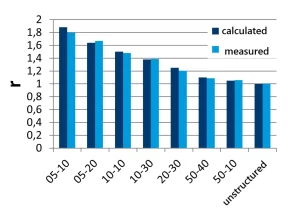
Dựa trên kích thước địa hình đo được của các mẫu, phần mềm sẽ xác định hệ số r được sử dụng trong phương trình Wenzel. Hình 4 cho thấy các hệ số r được xác định bằng thực nghiệm và các hệ số được tính theo hình dạng mục tiêu của các cấu trúc cho tất cả các mẫu được nghiên cứu. Các giá trị đo và lý thuyết khá phù hợp, sai số lớn nhất dưới 5% (mẫu 5-10).

Góc tiếp xúc

Để tìm hiểu xem độ thấm ướt của các mẫu có cấu trúc có tuân theo dự đoán của Wenzel hay không, các phép đo góc tiếp xúc được thực hiện với nước làm chất lỏng thử nghiệm (Hình 5). Đối với các cấu trúc có giá trị r thấp , cấu trúc vi mô hiển thị một phần trong hình ảnh thả (xem Hình 5).

Độ lệch được quy định theo Wenzel

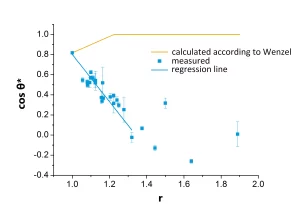
Kết quả của phép đo góc tiếp xúc được so sánh với giá trị r tương ứng của các mẫu trong Hình 6. Ngoài ra, đường đi dự kiến ​​dựa trên phương trình Wenzel được hiển thị ở đó, sử dụng góc tiếp xúc θ = 35,18°, được đo trên chip silicon không có cấu trúc. Có thể thấy rõ rằng so với xu hướng được dự đoán trên cơ sở lý thuyết của Wenzel, người ta quan sát thấy xu hướng ngược lại của các góc tiếp xúc thu được là hàm của r. Bề mặt ưa nước trở nên kỵ nước hơn và không ưa nước hơn do cấu trúc bề mặt.

Sự khác biệt giữa giá trị dự đoán và giá trị đo lường này có thể có nhiều nguyên nhân, sẽ vượt quá phạm vi của báo cáo này nếu được thảo luận chi tiết. Trong tài liệu khoa học có một số lượng lớn các ấn phẩm đề cập một cách toàn diện đến các điều kiện của các trạng thái Wenzel và Cassie-Baxter cũng như sự chuyển tiếp của chúng với nhau. Kết quả rõ ràng từ nghiên cứu là ngay cả với cấu trúc bề mặt được xác định rất rõ ràng và nước là chất lỏng thử nghiệm phổ biến nhất, việc dự đoán đơn giản về độ thấm ướt bằng phương trình Wenzel là không dễ dàng thực hiện được. Đúng là có những ví dụ trong đó mối quan hệ Wenzel cho phép dự đoán. Tuy nhiên, trên thực tế, không có cách nào khác ngoài việc đo góc tiếp xúc và đo cấu trúc bề mặt bằng phương pháp phù hợp như kính hiển vi đồng tiêu nếu cần có kết quả đáng tin cậy.

Phát triển một mô hình thực nghiệm như một giải pháp thay thế khả thi

Tuy nhiên, thực tế có liên quan là khả năng xác định mối quan hệ thực nghiệm giữa tham số r và góc tiếp xúc dựa trên kết quả đo được hiển thị ở đây. Điều này có thể được sử dụng trong ví dụ của chúng tôi để dự đoán ảnh hưởng của các cấu trúc bề mặt khác nhau đến độ thấm ướt hoặc để ngoại suy góc tiếp xúc trên bề mặt hoàn toàn không có cấu trúc ( r = 1) (xem Hình 6, độ khớp tuyến tính màu xanh nhạt). Điều này lại cho thấy ảnh hưởng của tiền xử lý chỉ đối với tính chất hóa học bề mặt mà không phụ thuộc vào hiệu ứng nhám.

Tóm tắt

Wenzel mô tả bằng một phương trình đơn giản độ nhám bề mặt r ảnh hưởng như thế nào đến độ ẩm của bề mặt xét theo góc tiếp xúc. Ở đây, phương trình này đã được thử nghiệm thực tế bằng cách đo góc tiếp xúc của nước trên các bề mặt được xác định rõ ràng có cùng thành phần hóa học nhưng độ nhám bề mặt khác nhau giữa r = 1 và r = 1,89. Nó đã chỉ ra rằng địa hình bề mặt của các mẫu cấu trúc vi mô có thể được xác định rất chính xác bằng cách sử dụng kính hiển vi đồng tiêu.

Trái ngược với dự đoán của phương trình Wenzel, xu hướng nghịch đảo của góc tiếp xúc với độ nhám tăng dần đã được quan sát bằng thực nghiệm. Độ ẩm được xác định bởi cả vật liệu của bề mặt và địa hình của nó. Nếu đã biết góc tiếp xúc trên bề mặt có cấu trúc, người ta sẽ không dựa vào khả năng dự đoán góc tiếp xúc Young trên bề mặt nhẵn của cùng vật liệu bằng phương trình Wenzel. Trên cơ sở các phép đo được mô tả, tính hợp lệ của phương trình Wenzel có thể được kiểm tra trong thực tế và, nếu cần, được thay thế bằng mối quan hệ thực nghiệm đơn giản (Hình 7). Đến lượt nó, điều này cho phép ngoại suy tính thấm ướt đối với các bề mặt không có cấu trúc và ước tính mức độ mà hóa học bề mặt và độ nhám bề mặt ảnh hưởng đến tính thấm ướt

Nguồn: https://www.kruss-scientific.com/en/know-how/application-reports/ar295-wetting-and-roughness-what-to-do-if-wenzel-does-not-work